High entropy (thermal equilibrium) for a gas means even distribution (due to repulsive force).
High entropy for large objects (planets galaxies) means clumping (attractive force).
But, Penrose: “The ‘lowness’ in the Sun’s entropy (considerable remoteness from thermal equilibrium) comes from a huge reservoir of low entropy that is potentially available in the uniformity of the gas from which the Sun has gravitationally condensed.” and this, confuses me.
For an answer to the apparent paradox of the fact that stars which are made out of condensed high entropy gas whose entropy (spatial degrees of freedom, i.e. Volume in phase space) decreases while the increase in momentum uncertainty (i.e. degrees of freedom of temperature) isn’t enough to counteract it, read this (it seems that the radiation of light from a star (low entropy radiation but in aggregate, enough of it) is what gives it a high overall entropy (this again is weird because a star is a low entropy beacon in space, for it to be high entropy because of the very fact that it is a beacon is ironic)).
2nd law implies initial state of universe was low (for it to increase).
But – the initial state of the universe was thermal equilibrium.
This is not a paradox, as the universe swells the new maximum possible equilibrium is higher – the actual entropy lags behind the maximum so the 2nd law holds.
The small size is not the main reason for the extremely low entropy pre-big bang singularity. As the universe expands, then contracts as black holes coagulate, the WEYL space-time curvature tensor -> infnity. In other words the end point of the universe is an extremely high entropy singularity. The initial state of the universe was WEYL = 0. Another space-time tensor, RICCI, starts at infinite levels and reduces to 0 as entropy increases.
[WEYL tensor is like Riemann curvature tensor, except that as it increases in value its RICCI curvature vanishes. The Reimann tensor is used to describe geometry because a single point in Reimann space can’t be represented by a single number. A manifold is a space which looks Euclidean at small scales but which can be more complicated at larger ones. A Reimann manifold is one where angles and distances can be defined (like the curved 2d space on a sphere where angles of a triangle add up to a known amount but which are less that 180 degrees?) (need to add a good definition of a tensor here e.g. Penrose graphical notation) ]Gravity causes matter to clump at large scales into stars, and big stars into black holes which have entropy values which are orders of magnitude higher than other elements in the universe (such as all of the photons in the background radiation) [this contradicts the measure below, need to resolve]
“Any region of the universe can be considered as an isolated cosmic box. The reason why entropy is increasing is because there are stars in that box. Hydrogen fuses to helium and nuclear energy is transformed into heat. Energy is released at the center of a star at millions of Kelvin and radiated away at thousands of Kelvin. Dissipative stars extract energy at high temperature and discard it at low temperature.
To measure entropy in cosmology we just need to count photons. If the number of photons in a given volume of the universe is N , then the entropy of that volume is S ~ k N where k is Boltzmann’s constant. The vast majority of the entropy of the universe is in the cosmic microwave background. Stars cannot change that. If all the matter in the universe were transformed into 3 K blackbody radiation, the number of photons would add up to only ~ 1 % of the number of CMB (cosmic background) photons. The entropy of the universe would increase by only 1%.”
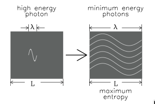
Living organisms near stars, increase the rate of entropy increase by directly or indirectly feeding on low entropy photons and radiating many more high entropy ones. Because there are more photons there are more degrees of freedom, therefore a larger volume in phase space (this is why bit splitting increases entropy).
Penrose: “The light from the sun brings energy to the earth in a comparatively low-entropy form, namely in the photons of visible light. The earth, including its inhabitants, does not retain this energy, but (after some while) re-radiates it all back into space. However, the re-radiated energy is in a high-entropy form, namely what is called ‘radiant heat’ – which means infra-red photons… the earth does not gain [net] energy from the sun! What the earth does is to take energy in low-entropy form, and then spew it all back again into space, but in a high-entropy form…To keep ourselves alive, we need to keep lowering the entropy that is within ourselves, we do not need to add to our energy content”.
As the nuclear reactions which balance the gravitational collapse in local clumps (stars) dwindle:
0 – 1.4 solar masses yields – red giant swells, burns, collapses on white dwarf core, eventually leaving black dwarf (burnt ember)
> 1.4 solar masses (above Chandrasekhar limit) Pauli’s exclusion principal cannot stop core collapse, supernova results, core collapses to neutron star (Pauli principal applied to Neutrons holds it apart, star is like a kilometer wide atomic nucleus)
> 2.5 solar masses (above Landau-Oppenheimer-Volkov limit) total collapse to black hole. Event horizon is point where escape velocity is greater than speed of light.
The entropy of a black hole is proportional to its area which is proportional to the square of its mass.
S = CA = Cm^2
Notes:
An increase in entropy corresponds to a loss of coherence.
*****************
black holes:
High entropy 1/4 of area of event horizon
Entropy comes from the boundary.
This makes sense- it is the ultimate self contained sytem and so has a perfect boundary.
It has info input. Does it have info output? (yes, evaporation via quantum tunneling)
It has v low temp – yes its all boundary, no bouncy balls inside.
Why is the infomation flow at small scale to do with repulsion (balls bouncing off each other) and at large scale, attraction – gravity.
Q. Is a black hole a possible universal turingmachine.